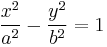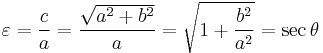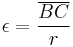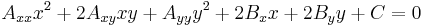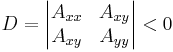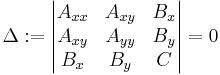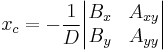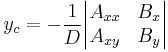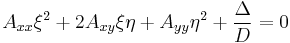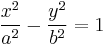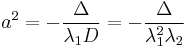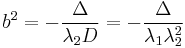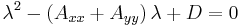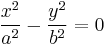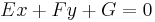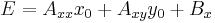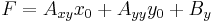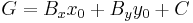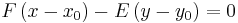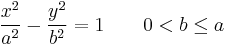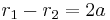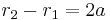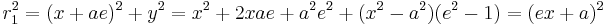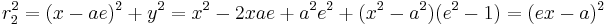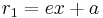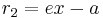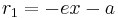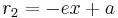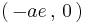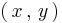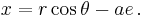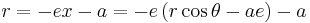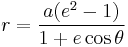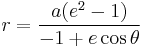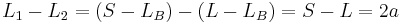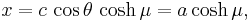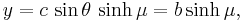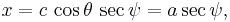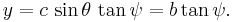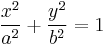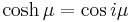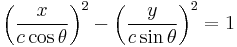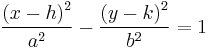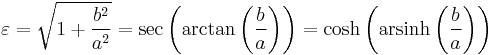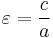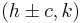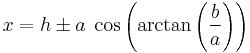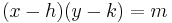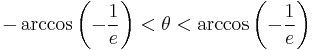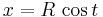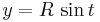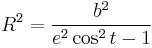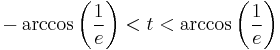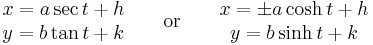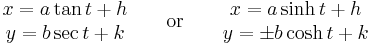Hyperbola
.png)
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror images of each other and resembling two infinite bows. The hyperbola is one of the four kinds of conic section, formed by the intersection of a plane and a cone. The other conic sections are the parabola, the ellipse, and the circle (the circle is a special case of the ellipse). Which conic section is formed depends on the angle the plane makes with the axis of the cone, compared with the angle a line on the surface of the cone makes with the axis of the cone. If the angle between the plane and the axis is less than the angle between the line on the cone and the axis, or if the plane is parallel to the axis, then the conic is a hyperbola.
Hyperbolas arise in practice in many ways: as the curve representing the function  in the Cartesian plane, as the appearance of a circle viewed from within it, as the path followed by the shadow of the tip of a sundial, as the shape of an open orbit (as distinct from a closed and hence elliptical orbit), such as the orbit of a spacecraft during a gravity assisted swing-by of a planet or more generally any spacecraft exceeding the escape velocity of the nearest planet, as the path of a single-apparition comet (one travelling too fast to ever return to the solar system), as the scattering trajectory of a subatomic particle (acted on by repulsive instead of attractive forces but the principle is the same), and so on.
in the Cartesian plane, as the appearance of a circle viewed from within it, as the path followed by the shadow of the tip of a sundial, as the shape of an open orbit (as distinct from a closed and hence elliptical orbit), such as the orbit of a spacecraft during a gravity assisted swing-by of a planet or more generally any spacecraft exceeding the escape velocity of the nearest planet, as the path of a single-apparition comet (one travelling too fast to ever return to the solar system), as the scattering trajectory of a subatomic particle (acted on by repulsive instead of attractive forces but the principle is the same), and so on.
Each branch of the hyperbola consists of two arms which become straighter (lower curvature) further out from the center of the hyperbola. Diagonally opposite arms one from each branch tend in the limit to a common line, called the asymptote of those two arms. There are therefore two asymptotes, whose intersection is at the center of symmetry of the hyperbola, which can be thought of as the mirror point about which each branch reflects to form the other branch. In the case of the curve  the asymptotes are the two coordinate axes.
the asymptotes are the two coordinate axes.
Hyperbolas share many of the ellipse's analytical properties such as eccentricity, focus, and directrix. Typically the correspondence can be made with nothing more than a change of sign in some term. Many other mathematical objects have their origin in the hyperbola, such as hyperbolic paraboloids (saddle surfaces), hyperboloids ("wastebaskets"), hyperbolic geometry (Lobachevsky's celebrated non-Euclidean geometry), hyperbolic functions (sinh, cosh, tanh, etc.), and gyrovector spaces (a non-Euclidean geometry used in both relativity and quantum mechanics).
History
The word "hyperbola" derives from the Greek ὑπερβολή, meaning "over-thrown" or "excessive", from which the English term hyperbole derives. The term hyperbola is believed to have been coined by Apollonius of Perga (ca. 262 BC–ca. 190 BC) in his definitive work on the conic sections, the Conics. For comparison, the other two general conic sections, the ellipse and the parabola, derive from the corresponding Greek words for "deficient" and "comparable"; these terms may refer to the eccentricity of these curves, which is greater than one (hyperbola), less than one (ellipse) and exactly one (parabola), respectively.
Nomenclature

Similar to a parabola, a hyperbola is an open curve, meaning that it continues indefinitely to infinity, rather than closing on itself as an ellipse does. A hyperbola consists of two disconnected curves called its arms or branches.
The closest distance of the two branches connecting their vertices is called the transverse axis or major axis corresponding to the major diameter of an ellipse. The midpoint of the transverse axis is known as the hyperbola's center. The distance a from the center to each vertex is sometimes called the major semi-axis. Outside of the transverse axis are the two focal points (foci) of the hyperbola. The line through these five points is one of the two principal axes of the hyperbola, the other being the bisection of the transverse axis. The hyperbola has mirror symmetry about its principal axes, and is also symmetric under a 180° turn about its center.
At large distances from the center, the hyperbola approaches two lines, its asymptotes, which intersect at the hyperbola's center. A hyperbola approaches its asymptotes arbitrarily closely as the distance from its center increases, but it never intersects them; however, a degenerate hyperbola consists only of its asymptotes. Consistent with the symmetry of the hyperbola, the slopes of the asymptotes are equal in magnitude but opposite in sign, ±b/a; the angle θ between the transverse axis and either asymptote equals arctan(b/a).
A conjugate axis of length 2b, corresponding to the minor axis of an ellipse, is sometimes drawn on the other principal axis but its endpoints have no special meaning. Because of that and of the minus sign in some of the formulas below, it is also called the imaginary axis of the hyperbola.
If b = a, the angle 2θ between the asymptotes equals 90° and the hyperbola is said to be rectangular or equilateral. If the transverse axis is aligned with the x-axis of a Cartesian coordinate system, the equation of a hyperbola centered on the origin can be written
A hyperbola aligned in this way is sometimes called an "East-West opening hyperbola"; by analogy, a hyperbola with its transverse axis aligned with the y-axis is called a "North-South opening hyperbola".

The shape of a hyperbola is defined entirely by its eccentricity ε, which is a dimensionless number always greater than one. The distance c from the center to the foci equals aε. The eccentricity can also be defined as the ratio of the distances to either focus and to a corresponding line known as the directrix; hence, the distance from the center to the directrices equals a/ε. In terms of the parameters a, b, c and the angle θ, the eccentricity equals
For example, the eccentricity of a rectangular hyperbola (θ = 45°, a = b) equals the square root of two, ε =  .
.
Every hyperbola has a conjugate hyperbola, in which the transverse and conjugate axes are exchanged without changing the asymptotes. This corresponds to exchanging a and b in the formulae describing the hyperbola; for example, the angle θ of the conjugate hyperbola equals 90° minus the angle of the original hyperbola. Thus, unless θ = 45° (a rectangular hyperbola), the angles in the original and conjugate hyperbolas differ, which implies that they have different eccentricities. Hence, the conjugate hyperbola does not correspond to a 90° rotation of the original hyperbola; the two hyperbolas are generally different in shape.
A few other lengths are used to describe hyperbolas. Consider a line perpendicular to the transverse axis (i.e., parallel to the conjugate axis) that passes through one of the hyperbola's foci. The line segment connecting the two intersection points of this line with the hyperbola is known as the latus rectum and has a length 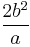 . The semi-latus rectum l is half of this length, i.e.,
. The semi-latus rectum l is half of this length, i.e., 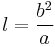 . The focal parameter p is the distance from a focus to its corresponding directrix, and equals
. The focal parameter p is the distance from a focus to its corresponding directrix, and equals 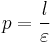 .
.
Mathematical definitions
A hyperbola can be defined mathematically in several equivalent ways.
Conic section

A hyperbola may be defined as the curve of intersection between a right circular conical surface and a plane that cuts through both halves of the cone. The other major types of conic sections are the ellipse and the parabola; in these cases, the plane cuts through only one half of the double cone. If the plane is parallel to the axis of the double cone and passes through its central apex, a degenerate hyperbola results that is simply two straight lines that cross at the apex point.
Difference of distances to foci
A hyperbola may be defined equivalently as the locus of points where the difference of the distances to the two foci is a constant equal to 2a, the distance between its two vertices. This definition accounts for many of the hyperbola's applications, such as trilateration; this is the problem of determining position from the difference in arrival times of synchronized signals, as in GPS.
This definition may be expressed also in terms of tangent circles. The center of any circles externally tangent to two given circles lies on a hyperbola, whose foci are the centers of the given circles and where the vertex distance 2a equals the difference in radii of the two circles. As a special case, one given circle may be a point located at one focus; since a point may be considered as a circle of zero radius, the other given circle—which is centered on the other focus—must have radius 2a. This provides a simple technique for constructing a hyperbola, as shown below. It follows from this definition that a tangent line to the hyperbola at a point P bisects the angle formed with the two foci, i.e., the angle F1P F2. Consequently, the feet of perpendiculars drawn from each focus to such a tangent line lies on a circle of radius a that is centered on the hyperbola's own center.
A proof that this characterization of the hyperbola is equivalent to the conic-section characterization can be done without coordinate geometry by means of Dandelin spheres.
Directrix
The locus of points for which the ratio of the distances to one focus and to a line (called the directrix) is a constant larger than 1. This constant is the eccentricity of the hyperbola.
Reciprocation of a circle
The reciprocation of a circle B in a circle C always yields a conic section such as a hyperbola. The process of "reciprocation in a circle C" consists of replacing every line and point in a geometrical figure with their corresponding pole and polar, respectively. The pole of a line is the inversion of its closest point to the circle C, whereas the polar of a point is the converse, namely, a line whose closest point to C is the inversion of the point.
The eccentricity of the conic section obtained by reciprocation is the ratio of the distances between the two circles' centers to the radius r of reciprocation circle C. If B and C represent the points at the centers of the corresponding circles, then
Since the eccentricity of a hyperbola is always greater than one, the center B must lie outside of the reciprocating circle C.
This definition implies that the hyperbola is both the locus of the poles of the tangent lines to the circle B, as well as the envelope of the polar lines of the points on B. Conversely, the circle B is the envelope of polars of points on the hyperbola, and the locus of poles of tangent lines to the hyperbola. Two tangent lines to B have no (finite) poles because they pass through the center C of the reciprocation circle C; the polars of the corresponding tangent points on B are the asymptotes of the hyperbola. The two branches of the hyperbola correspond to the two parts of the circle B that are separated by these tangent points.
Quadratic equation
A hyperbola can also be defined as a second-degree equation in the Cartesian coordinates (x, y) of the plane
provided that the constants Axx, Axy, Ayy, Bx, By, and C satisfy the determinant condition
A special case of a hyperbola—the degenerate hyperbola consisting of two intersecting lines—occurs when another determinant is zero
This determinant Δ is sometimes called the discriminant of the conic section.[1]
The center (xc, yc) of the hyperbola may be determined from the formulae
In terms of new coordinates, ξ = x − xc and η = y − yc, the defining equation of the hyperbola can be written
The principal axes of the hyperbola make an angle Φ with the positive x-axis that equals
Rotating the coordinate axes so that the x-axis is aligned with the transverse axis brings the equation into its standard form
The major and minor semiaxes a and b are defined by the equations
where λ1 and λ2 are the roots of the quadratic equation
For comparison, the corresponding equation for a degenerate hyperbola is
The tangent line to a given point (x0, y0) on the hyperbola is defined by the equation
where E, F and G are defined
The normal line to the hyperbola at the same point is given by the equation
The normal line is perpendicular to the tangent line, and both pass through the same point (x0, y0).
From the equation
the basic property that with  and
and  being the distances from a point
being the distances from a point 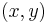 to the left focus
to the left focus 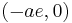 and the right focus
and the right focus 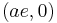 one has for a point on the right branch that
one has for a point on the right branch that
and for a point on the left branch that
can be proved as follows:
If x,y is a point on the hyperbola the distance to the left focal point is
To the right focal point the distance is
If x,y is a point on the right branch of the hyperbola then 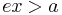 and
and
Subtracting these equations one gets
If x,y is a point on the left branch of the hyperbola then 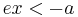 and
and
Subtracting these equations one gets
The true anomaly

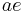 The x-coordinate is
The x-coordinate is 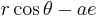
The polar angle 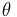 of a point on a hyperbola relative the focal point
of a point on a hyperbola relative the focal point  is called the true anomaly of the point. Relative the "canonical coordinate system" with origin at the mid-point between the foci
is called the true anomaly of the point. Relative the "canonical coordinate system" with origin at the mid-point between the foci 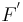 and
and  in which the equation of the hyperbola is
in which the equation of the hyperbola is
the coordinates of the left focal point is
For a point
on the left branch of the hyperbola one has that
As
one has that
This is the representation of the near branch of a hyperbola in polar coordinates with respect to a focal point.
The representation of the far branch is[2]:
Geometrical constructions
Similar to the ellipse, a hyperbola can be constructed using a taut thread. A straightedge of length S is attached to one focus F1 at one of its corners A so that it is free to rotate about that focus. A thread of length L = S - 2a is attached between the other focus F2 and the other corner B of the straightedge. A sharp pencil is held up against the straightedge, sandwiching the thread tautly against the straightedge. Let the position of the pencil be denoted as P. The total length L of the thread equals the sum of the distances L2 from F2 to P and LB from P to B. Similarly, the total length S of the straightedge equals the distance L1 from F1 to P and LB. Therefore, the difference in the distances to the foci, L1 − L2 equals the constant 2a
A second construction uses intersecting circles, but is likewise based on the constant difference of distances to the foci. Consider a hyperbola with two foci F1 and F2, and two vertices P and Q; these four points all lie on the transverse axis. Choose a new point T also on the transverse axis and to the right of the rightmost vertex P; the difference in distances to the two vertices, QT − PT = 2a, since 2a is the distance between the vertices. Hence, the two circles centered on the foci F1 and F2 of radius QT and PT, respectively, will intersect at two points of the hyperbola.
A third construction relies on the definition of the hyperbola as the reciprocation of a circle. Consider the circle centered on the center of the hyperbola and of radius a; this circle is tangent to the hyperbola at its vertices. A line g drawn from one focus may intersect this circle in two points M and N; perpendiculars to g drawn through these two points are tangent to the hyperbola. Drawing a set of such tangent lines reveals the envelope of the hyperbola.
Geometrical properties
The ancient Greek geometers recognized a reflection property of hyperbolas. If a ray of light emerges from one focus and is reflected from the hyperbola, the light-ray appears to have come from the other focus. Equivalently, by reversing the direction of the light, rays directed at one of the foci from the exterior of the hyperbola are reflected towards the other focus. This property is analogous to the property of ellipses that a ray emerging from one focus is reflected from the ellipse directly towards the other focus (rather than away as in the hyperbola). Expressed mathematically, lines drawn from each focus to the same point on the hyperbola intersect at equal angles; the tangent line to a hyperbola at a point P bisects the angle formed with the two foci, F1PF2.
Tangent lines to a hyperbola have another remarkable geometrical property. If a tangent line at a point T intersects the asymptotes at two points K and L, then T bisects the line segment KL, and the product of distances to the hyperbola's center, OK×OL is a constant.
Hyperbolic functions and equations
Just as the sine and cosine functions give a parametric equation for the ellipse, so the hyperbolic sine and hyperbolic cosine give a parametric equation for the hyperbola. Assuming that the foci lie at ±c on the x-axis, the Cartesian coordinates of one branch of the hyperbola can be expressed as
where μ varies over the real numbers, and θ is the angle of the asymptotes with the line of foci. To generate both branches of the hyperbola, the parametric equation can be expressed in terms of the secant and tangent trigonometric functions
Relation with other conic sections
There are three major types of conic sections: hyperbolas, ellipses and parabolas. Since the parabola may be seen as a limiting case poised exactly between an ellipse and a hyperbola, there are effectively only two major types, ellipses and hyperbolas. These two types are related in that formulae for one type can often be applied to the other.
The basic equation for a hyperbola
may be seen as a version of the corresponding ellipse equation
in which the semi-minor axis length b is imaginary. Similarly, the parametric equations for a hyperbola and an ellipse are expressed in terms of hyperbolic and trigonometric functions, respectively, which are again related by an imaginary number, e.g.,
Hence, many formulae for the ellipse can be extended to hyperbolas by adding the imaginary unit i in front of the semi-minor axis b and the angle. For example, the arclength of a segment of an ellipse can be determined using an incomplete elliptic integral of the second kind. The corresponding arclength of a hyperbola is given by the same function with imaginary parameters b and μ, namely, ib E(iμ, c).
Conic section analysis of the hyperbolic appearance of circles

Besides providing a uniform description of circles, ellipses, parabolas, and hyperbolas, conic sections can also be understood as a natural model of the geometry of perspective in the case where the scene being viewed consists of a circle, or more generally an ellipse. The viewer is typically a camera or the human eye. In the simplest case the viewer's lens is just a pinhole; the role of more complex lenses is merely to gather far more light while retaining as far as possible the simple pinhole geometry in which all rays of light from the scene pass through a single point. Once through the lens, the rays then spread out again, in air in the case of a camera, in the vitreous humor in the case of the eye, eventually distributing themselves over the film, imaging device, or retina, all of which come under the heading of image plane. The lens plane is a plane parallel to the image plane at the lens; all rays pass through a single point on the lens plane, namely the lens itself.
When the circle directly faces the viewer, the viewer's lens is on-axis, meaning on the line normal to the circle through its center (think of the axle of a wheel). The rays of light from the circle through the lens to the image plane then form a cone with circular cross section whose apex is the lens. The image plane concretely realizes the abstract cutting plane in the conic section model.
When in addition the viewer directly faces the circle, the circle is rendered faithfully on the image plane without perspective distortion, namely as a scaled-down circle. When the viewer turns attention or gaze away from the center of the circle the image plane then cuts the cone in an ellipse, parabola, or hyperbola depending on how far the viewer turns, corresponding exactly to what happens when the surface cutting the cone to form a conic section is rotated.
A parabola arises when the lens plane is tangent to (touches) the circle. A viewer with perfect 180-degree wide-angle vision will see the whole parabola; in practice this is impossible and only a finite portion of the parabola is captured on the film or retina.
When the viewer turns further so that the lens plane cuts the circle in two points, the shape on the image plane becomes that of a hyperbola. The viewer still sees only a finite curve, namely a portion of one branch of the hyperbola, and is unable to see the second branch at all, which corresponds to the portion of the circle behind the viewer, more precisely, on the same side of the lens plane as the viewer. In practice the finite extent of the image plane makes it impossible to see any portion of the circle near where it is cut by the lens plane. Further back however one could imagine rays from the portion of the circle well behind the viewer passing through the lens, were the viewer transparent. In this case the rays would pass through the image plane before the lens, yet another impracticality ensuring that no portion of the second branch could possibly be visible.
The tangents to the circle where it is cut by the lens plane constitute the asymptotes of the parabola. Were these tangents to be drawn in ink in the plane of the circle, the eye would perceive them as asymptotes to the visible branch. Whether they converge in front of or behind the viewer depends on whether the lens plane is in front of or behind the center of the circle respectively.
If the circle is drawn on the ground and the viewer gradually transfers gaze from straight down at the circle up towards the horizon, the lens plane eventually cuts the circle producing first a parabola then a hyperbola on the image plane. As the gaze continues to rise the asymptotes of the hyperbola, if realized concretely, appear coming in from left and right, swinging towards each other and converging at the horizon when the gaze is horizontal. Further elevation of the gaze into the sky then brings the point of convergence of the asymptotes towards the viewer.
By the same principle with which the back of the circle appears on the image plane were all the physical obstacles to its projection to be overcome, the portion of the two tangents behind the viewer appear on the image plane as an extension of the visible portion of the tangents in front of the viewer. Like the second branch this extension materializes in the sky rather than on the ground, with the horizon marking the boundary between the physically visible (scene in front) and invisible (scene behind), and the visible and invisible parts of the tangents combining in a single X shape. As the gaze is raised and lowered about the horizon, the X shape moves oppositely, lowering as the gaze is raised and vice versa but always with the visible portion being on the ground and stopping at the horizon, with the center of the X being on the horizon when the gaze is horizontal.
All of the above was for the case when the circle faces the viewer, with only the viewer's gaze varying. When the circle starts to face away from the viewer the viewer's lens is no longer on-axis. In this case the cross section of the cone is no longer a circle but an ellipse (never a parabola or hyperbola). However the principle of conic sections does not depend on the cross section of the cone being circular, and applies without modification to the case of eccentric cones.
It is not difficult to see that even in the off-axis case a circle can appear circular, namely when the image plane (and hence lens plane) is parallel to the plane of the circle. That is, to see a circle as a circle when viewing it obliquely, look not at the circle itself but at the plane in which it lies. From this it can be seen that when viewing a plane filled with many circles, all of them will appear circular simultaneously when the plane is looked at directly.
A common misperception about the hyperbola is that it is a mathematical curve rarely if ever encountered in daily life. The reality is that one sees a hyperbola whenever catching sight of portion of a circle cut by one's lens plane (and a parabola when the lens plane is tangent to, i.e. just touches, the circle). The inability to see very much of the arms of the visible branch, combined with the complete absence of the second branch, makes it virtually impossible for the human visual system to recognize the connection with hyperbolas such as y = 1/x where both branches are on display simultaneously.
Coordinate systems
A family of confocal hyperbolas is the basis of the system of elliptic coordinates in two dimensions. These hyperbolas are described by the equation
where the foci are located at a distance c from the origin on the x-axis, and where θ is the angle of the asymptotes with the x-axis. Every hyperbola in this family is orthogonal to every ellipse that shares the same foci. This orthogonality may be shown by a conformal map of the Cartesian coordinate system w = z + 1/z, where z= x + iy are the original Cartesian coordinates, and w=u + iv are those after the transformation.
Other orthogonal two-dimensional coordinate systems involving hyperbolas may be obtained by other conformal mappings. For example, the mapping w = z2 transforms the Cartesian coordinate system into two families of orthogonal hyperbolas.
Applications
Hyperbolas may be seen in many sundials. On any given day, the sun revolves in a circle on the celestial sphere, and its rays striking the point on a sundial traces out a cone of light. The intersection of this cone with the horizontal plane of the ground forms a conic section, by definition. At most populated latitudes and at most times of the year, this conic section is a hyperbola. In practical terms, the shadow of the tip of a pole traces out a hyperbola on the ground over the course of a day. The shape of this hyperbola varies with the geographical latitude and with the time of the year, since those factors affect the cone of the sun's rays relative to the horizon. The collection of such hyperbolas for a whole year at a given location was called a pelekinon by the Greeks, since it resembles a double-bladed axe.
A hyperbola is the basis for solving trilateration problems, the task of locating a point from the differences in its distances to given points — or, equivalently, the difference in arrival times of synchronized signals between the point and the given points. Such problems are important in navigation, particularly on water; a ship can locate its position from the difference in arrival times of signals from a LORAN or GPS transmitters. Conversely, a homing beacon or any transmitter can be located by comparing the arrival times of its signals at two separate receiving stations; such techniques may be used to track objects and people. In particular, the set of possible positions of a point that has a distance difference of 2a from two given points is a hyperbola of vertex separation 2a whose foci are the two given points.
The paths followed by any particle in the classical Kepler problem is a conic section. In particular, if the total energy E of the particle is greater than zero (i.e., if the particle is unbound), the path of such a particle is a hyperbola. This property is useful in studying atomic and sub-atomic forces by scattering high-energy particles; for example, the Rutherford experiment demonstrated the existence of an atomic nucleus by examining the scattering of alpha particles from gold atoms. If the short-range nuclear interactions are ignored, the atomic nucleus and the alpha particle interact only by a repulsive Coulomb force, which satisfies the inverse square law requirement for a Kepler problem.
As shown first by Apollonius of Perga, a hyperbola can be used to trisect any angle, a intensely studied problem of geometry. Given an angle, one first draws a circle centered on its middle point O, which intersects the legs of the angle at points A and B. One next draws the line through A and B and constructs a hyperbola of eccentricity ε=2 with that line as its transverse axis and B as one focus. The directrix of the hyperbola is the bisector of AB, and for any point P on the hyperbola, the angle ABP is twice as large as the angle BAP. Let P be a point on the circle. By the inscribed angle theorem, the corresponding center angles are likewise related by a factor of two, AOP = 2×POB. But AOP+POB equals the original angle AOB. Therefore, the angle has been trisected, since 3×POB = AOB.
Derived curves
Several other curves can be derived from the hyperbola by inversion, the so-called inverse curves of the hyperbola. If the center of inversion is chosen as the hyperbola's own center, the inverse curve is the lemniscate of Bernoulli; the lemniscate is also the envelope of circles centered on a rectangular hyperbola and passing through the origin. If the center of inversion is chosen at a focus or a vertex of the hyperbola, the resulting inverse curves are a limaçon or a strophoid, respectively.
Extensions
The three-dimensional analog of a hyperbola is a hyperboloid. Hyperboloid come in two varieties, those of one sheet and those of two sheets. A simple way of producing a hyperboloid is to rotate a hyperbola about the axis of its foci or about its symmetry axis perpendicular to the first axis; these rotations produce hyperboloids of two and one sheet, respectively.
Equations for special cases
In Cartesian coordinates
East-west opening hyperbola centered at (h,k):
The major axis runs through the center of the hyperbola and intersects both arms of the hyperbola at the vertices (bend points) of the arms. The foci lie on the extension of the major axis of the hyperbola.
The minor axis runs through the center of the hyperbola and is perpendicular to the major axis.
In both formulas a is the semi-major axis (half the distance between the two arms of the hyperbola measured along the major axis)[3], and b is the semi-minor axis.
If one forms a rectangle with vertices on the asymptotes and two sides that are tangent to the hyperbola, the length of the sides tangent to the hyperbola are 2b in length while the sides that run parallel to the line between the foci (the major axis) are 2a in length. Note that b may be larger than a despite the names minor and major.
If one calculates the distance from any point on the hyperbola to each focus, the absolute value of the difference of those two distances is always 2a.
The eccentricity is given by
If c equals the distance from the center to either focus, then
where
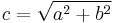 .
.
The distance c is known as the linear eccentricity of the hyperbola. The distance between the foci is 2c or 2aε.
The foci for an east-west opening hyperbola are given by
and for a north-south opening hyperbola are given by
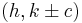 .
.
The directrices for an east-west opening hyperbola are given by
and for a north-south opening hyperbola are given by
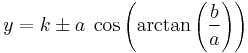 .
.
Cartesian (rectangular hyperbola with horizontal/vertical asymptotes)

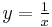 , the reciprocal function
, the reciprocal functionFor rectangular hyperbolas with the coordinate axes parallel to their asymptotes:
These are equilateral hyperbolas (eccentricity 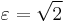 ) with semi-major axis and semi-minor axis given by
) with semi-major axis and semi-minor axis given by 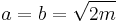 .
.
The simplest example of these are the hyperbolas
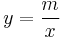 .
.
describing quantities x and y that are inversely proportional.
In polar coordinates
The polar coordinates used most commonly for the hyperbola are defined relative to the Cartesian coordinate system that has its origin in a focus and its x-axis pointing towards the origin of the "canonical coordinate system" as illustrated in the figure of the section "True anomaly".
Relative to this coordinate system one has that
and the range of the true anomaly 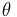 is:
is:
With polar coordinate relative to the "canonical coordinate system"
one has that
For the right branch of the hyperbola the range of 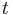 is:
is:
Parametric equations
East-west opening hyperbola:
North-south opening hyperbola:
In all formulae (h,k) are the center coordinates of the hyperbola, a is the length of the semi-major axis, and b is the length of the semi-minor axis.
See also
- Parabola
- Circle
- Ellipse
- Hyperbolic sector
- Hyperbolic angle
- Hyperbolic function
- Hyperbolic growth
- Hyperbolic partial differential equation
- Hyperbolic structure
- Hyperbolic trajectory
- Hyperboloid
- Multilateration
- Apollonius of Perga, the Greek geometer who gave the ellipse, parabola, and hyperbola the names by which we know them.
- Elliptic coordinates, an orthogonal coordinate system based on families of ellipses and hyperbolae.
References
- ↑ Korn and Korn, p. 40.
- ↑ [www.oup.com/uk/orc/bin/9780199289295/woolfson_ch10.pdf Conic sections and orbits]
- ↑ In some literature the value of a is taken negative for a hyperbola (the negative of half the distance between the two arms of the hyperbola measured along the major axis). This allows some formulas to be applicable to ellipses as well as to hyperbolas.
External links
- Apollonius' Derivation of the Hyperbola at Convergence
- Unit hyperbola on PlanetMath
- Conic section on PlanetMath
- Conjugate hyperbola on PlanetMath
- Mathworld - Hyperbola